<等差数列の公式>
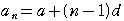 ,
,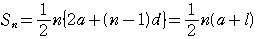
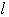 :末項
:末項
<等比数列の公式>
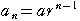 ,
,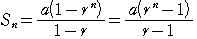
<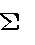 の公式>
の公式>
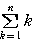 =
=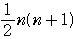 ,
,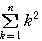 =
=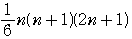 ,
,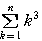 =
=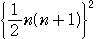
 の公式は
の公式は
もう覚えてくれたことと思うが,この公式が
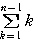
 になるともうわからない人がいる。
になるともうわからない人がいる。
確かに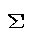 の記号はわかりにくいので,この記号を使わずに書けばよい。
の記号はわかりにくいので,この記号を使わずに書けばよい。
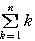 =
=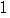 +
+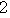 +
+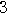 +…+
+…+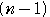 +
+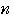 ,
,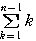 =
=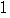 +
+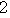 +
+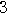 +…+
+…+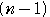
 となる。よって,
となる。よって,
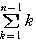 =
=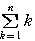 −
−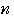 =
=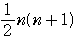 −
−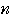 =
=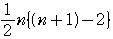 =
=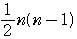 =
=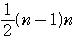
 となり,
となり,
公式
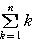 =
=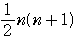
 において,
において,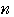
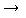
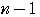
 を代入したものになる。
を代入したものになる。
同様にして,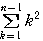 =
=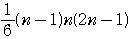 ,
,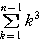 =
=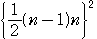
 となる。
となる。

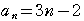
 のとき,
のとき,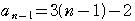 =
=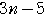
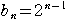
 のとき,
のとき,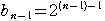 =
=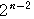 なども同様である。
なども同様である。
<階差数列の公式>
数列
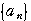
 の階差数列
の階差数列
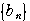
 とするとき,
とするとき,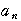 =
=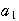 +
+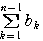
 は,
は,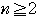
 のとき
のとき
成立する公式であって,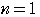
 のときは別に調べなければならなかった。
のときは別に調べなければならなかった。
しかし,今まで解いた問題ではいつも不思議に
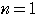
 のときにも成立していた。
のときにも成立していた。
もしかしたら,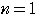
 のときには成立しないような例はないのではないかという
のときには成立しないような例はないのではないかという
気がしてくる。
次の数列を考えてみよう。
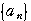 :0,1,1,1,………
:0,1,1,1,……… 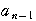 ,
,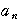 ,
,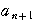
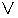
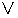
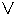
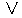
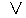
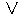
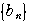 :
:  1,0,0,0,………
1,0,0,0,……… 
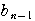
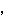
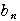
この数列の階差数列
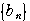
 は,
は,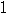 ,
,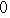 ,
,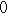 ,
,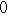 ,… だから,
,… だから,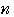
 に関係なく
に関係なく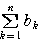 =
=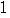
となる。すなわち,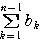 =
=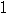 より,
より,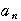 =
=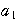 +
+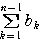
 =
=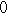 +
+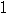 =
=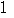 となり,
となり,
これは
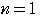
 のときには成立しない。
のときには成立しない。
階差数列の定義
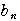 =
=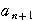 −
−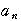
 より,
より,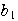 =
=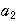 −
−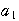
 までは定義されるので,
までは定義されるので,
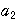 =
=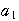 +
+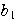 ,
,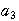 =
=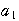 +
+
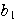 +
+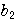
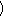 ,………,
,………,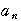 =
=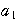 +
+
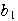 +
+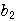 +…+
+…+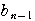
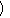
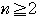
 のときは階差数列の公式を用いてもよいが,
のときは階差数列の公式を用いてもよいが,
初項の
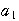
 については,その前の項を引くわけにはいかないので,
については,その前の項を引くわけにはいかないので,
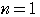
 のときは別に考える必要があるわけである。
のときは別に考える必要があるわけである。
<漸化式の解法>:隣接2項間漸化式など,種々の漸化式を8パターンに分類した解法
<隣接3項間漸化式の解法>:特性方程式による解法
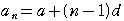 ,
,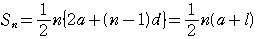
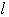 :末項
:末項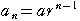 ,
,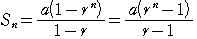
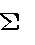 の公式>
の公式>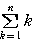 =
=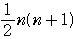 ,
,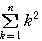 =
=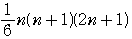 ,
,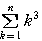 =
=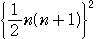
 の公式は
の公式は
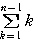
 になるともうわからない人がいる。
になるともうわからない人がいる。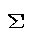 の記号はわかりにくいので,この記号を使わずに書けばよい。
の記号はわかりにくいので,この記号を使わずに書けばよい。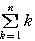 =
=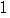 +
+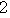 +
+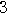 +…+
+…+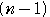 +
+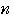 ,
,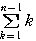 =
=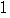 +
+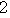 +
+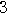 +…+
+…+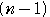
 となる。よって,
となる。よって,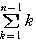 =
=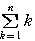 −
−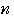 =
=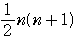 −
−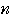 =
=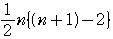 =
=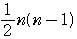 =
=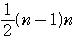
 となり,
となり,
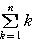 =
=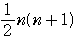
 において,
において,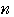
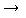
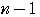
 を代入したものになる。
を代入したものになる。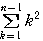 =
=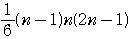 ,
,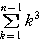 =
=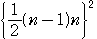
 となる。
となる。
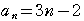
 のとき,
のとき,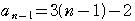 =
=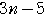
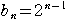
 のとき,
のとき,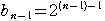 =
=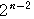 なども同様である。
なども同様である。
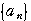
 の階差数列
の階差数列
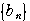
 とするとき,
とするとき,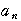 =
=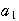 +
+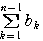
 は,
は,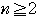
 のとき
のとき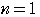
 のときは別に調べなければならなかった。
のときは別に調べなければならなかった。
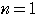
 のときにも成立していた。
のときにも成立していた。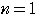
 のときには成立しないような例はないのではないかという
のときには成立しないような例はないのではないかという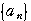 :0,1,1,1,………
:0,1,1,1,……… 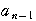 ,
,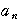 ,
,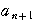
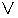
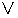
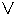
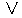
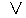
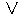
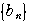 :
:  1,0,0,0,………
1,0,0,0,……… 
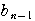
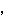
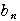

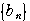
 は,
は,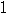 ,
,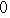 ,
,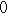 ,
,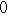 ,… だから,
,… だから,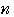
 に関係なく
に関係なく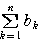 =
=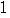
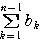 =
=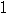 より,
より,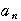 =
=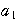 +
+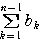
 =
=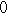 +
+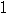 =
=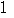 となり,
となり,
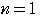
 のときには成立しない。
のときには成立しない。
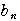 =
=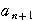 −
−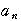
 より,
より,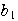 =
=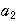 −
−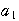
 までは定義されるので,
までは定義されるので,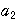 =
=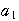 +
+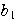 ,
,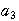 =
=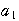 +
+
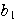 +
+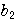
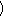 ,………,
,………,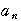 =
=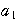 +
+
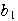 +
+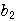 +…+
+…+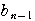
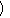
 のときは階差数列の公式を用いてもよいが,
のときは階差数列の公式を用いてもよいが,
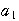
 については,その前の項を引くわけにはいかないので,
については,その前の項を引くわけにはいかないので,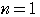
 のときは別に考える必要があるわけである。
のときは別に考える必要があるわけである。